Gegeven is u(n) = n2/2n, dan is u(n+1) = (n+1)2/2n+1, zodat v(n):
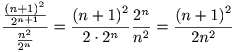
Geraak je nu tot het opgegeven antwoord?
mvg,
Tom
td
20-2-2007
gegeven de rij u(n)=n2/2n.
om te bewijzen dat limiet n naar oneindig:n2/2n is 0 gebruiken we de rij v(n)=u(n+1)/u(n)
Toon aan dat v(n)=0,5[1+(1/n)]2
Kunt U uitleggen hoe dit werkt?Piet
20-2-2007
Beste Piet,
Gegeven is u(n) = n2/2n, dan is u(n+1) = (n+1)2/2n+1, zodat v(n):
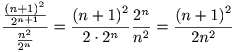
Geraak je nu tot het opgegeven antwoord?
mvg,
Tom
td
20-2-2007
#49313 - Rijen en reeksen - Leerling bovenbouw havo-vwo