WisFaq!

Delta-epsilon methode

Ik moet de limiet van x naar 1 van 1/(1+x²) = ¹/₂ bewijzen met behulp van de delta-epsilon methode. Hoe werkt dat? Kan iemand die voormaken?

Leen
14-2-2007

Antwoord

Beste Leen,

Uitschrijven van de epsilon-delta definitie levert:



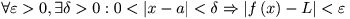
Met a = 1 en L = 1/2 krijgen we voor dat tweede deel:



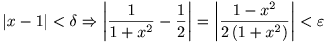
De teller kan je ontbinden in (1-x)(1+x).
We hebben reeds dat: |x-1| = |1-x| d

Hieruit volgt: 1-d x 1+d Û 2-d x+1 2+d Þ |x+1| 2+d

Met d1 is d²d en kunnen we afschatten: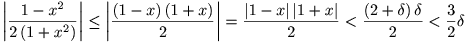



Voor een opgegeven e>0 kiezen we d = min(2e/3,1) zodat het gevraagde volgt. Met dank aan collega kphart voor de verbetering.

mvg,
Tom

td
18-2-2007