WisFaq!

Re: Re: Re: Re: Primitieven

wederom waarschijnlijk een domme vraag, maar is dan nu de algemene formule voor de primitieven van 1/ax²+bx+c --^4a2/_4ac-b²arctan(^x+b/_2a/_{Ö^4ac-b2/4a²}??? Sorry dat ik zo lastig ben;)

arie
13-2-2007

Antwoord

Beste Arie,

Bijna, de primitieve van 1/(x²+1) is arctan(x), maar van 1/((px+q)²+1) is arctan(px+q)/p. Als argument van de arctangens krijg je dus alles wat binnen het kwadraat staat maar je moet nog delen door de coëfficiënt van x (door de substitutieregel).

Als je de uitdrukking onder het kwadraat vereenvoudigt, vind je:



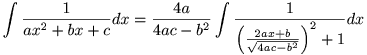
Integreren kan, eventueel na substitutie, door te delen door de coëfficiënt van x, je krijgt dus de arctangens van de uitdrukking onder het kwadraat:



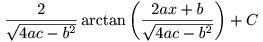
mvg,
Tom

td
13-2-2007