WisFaq!

Domein en bereik arctan

Waarom heeft de functie f(x)=arctan als domein $\mathbf{R}$ en als bereik (-0.5$\pi$,0.5$\pi$)? Hier moet volgens mijn boek een verklaring voor zijn, maar ik kan er niet op komen. Kunt u mij helpen? Alvast bedankt

Maarten Hoek
5-2-2007

Antwoord

Beste Maarten,

De arctan is de inverse functie van de tangensfunctie.
Zoals je misschien weet, kun je de inverse van een functie krijgen door de functie die je wil inverteren te spiegelen in de lijn y = x.
Je weet dat de tangensfunctie 'zichzelf voortdurend herhaalt'.



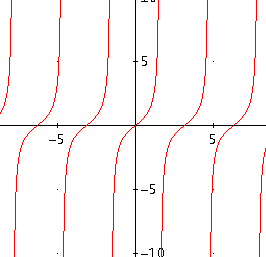
Als we die oneindige grafiek zouden spiegelen in de lijn y = x dan krijg je als inverse geen functie (maar een relatie), want er zijn meerdere y-waarden bij eenzelfde x-waarde.

Om er nu voor te zorgen dat er een functie als inverse uitkomt, gaan we ervoor zorgen dat de oorspronkelijke functie (de tangensfunctie) injectief en surjectief is (dat wil zeggen verschillende x-waarden hebben verschillende y-waarden en elke mogelijke y-waarde wordt aangenomen). Als een functie injectief en surjectief is, noem je 'm ook wel bijectief.
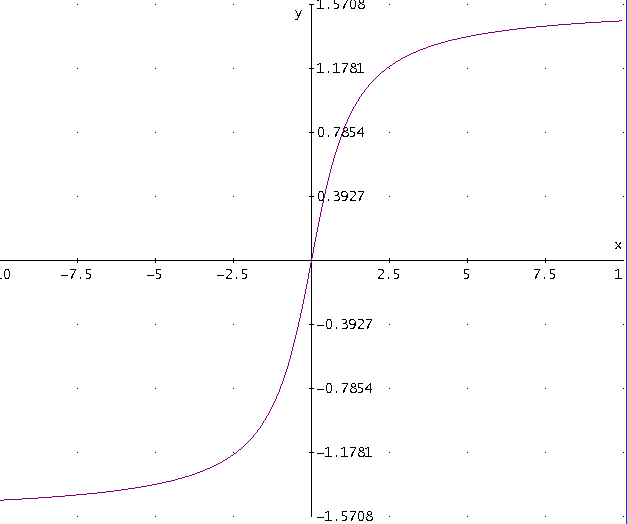
Als we het x-interval $<$-$\pi$/2,$\pi$/2$>$ kiezen dan heeft elke x-waarde een verschillende y-waarde (dus injectief) én elke mogelijke y-waarde wordt aangenomen. Dus domein is $<$-$\pi$/2,$\pi$/2$>$ en het bereik is $\mathbf{R}$.

Als we dit gedeelte van de tangensgrafiek nu spiegelen in de lijn y = x krijgen we de functie arctan(x). Hierbij geldt dat het domein van tan(x) je bereik is geworden en je bereik is je domein geworden. Zie onderstaande tekening van de arctan.



Groetjes,

Davy.

Davy
5-2-2007