WisFaq!

Rate of change, richtings afgeleide

Graag wil ik de rate of change (ik weet niet wat het in het nederlands is) uitrekenen van

f(x,y)=y⁴+2xy³+(x²)(y²) in (0,1) in de richting van I+2J

wat ik zelf kan bedenken:

delta f(x,y)=(2x³+2xy²)I + (4y³+6xy²+2x²y)J
in punt (0,1) geeft dit 2I+4J

dan komt m'n probleem.

Ik moet nu ((I+2J)/(|I+2J|)) · (2I+4J)

dit kan ik dan uitwerken tot (2I²+8IJ+8J)/(|I+2J|) maar volgens mij staat hier dan onzin.

Help?

ronald
29-1-2007

Antwoord

In de omschrijving van het vraagstuk zeg je dat het gaat om de richting I+2J.
In je wiskundeboek wordt dit waarschijnlijk geschreven als:
i+2j. De i en de j stellen de eenheidsvectoren voor in resp. de x- en de y-richting.
Dus i=(1,0,0) en j=(0,1,0)

voorts reken de delta f(x,y) uit. Wat je bedoelt, is 'grad', ofwel nabla, ofwel Ñ = (¶f/¶x, ¶f/¶y, ¶f/¶z).
Delta, Laplace operator is iets anders.
Df º Ѳf = ¶²f/¶x² + ¶²f/¶y² + ¶²f/¶z²

Als je Ñf(x,y) uitrekent, levert je dat een vector op:

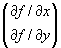
In feite wordt deze dus uitgesponnen in 2 delen:
...=

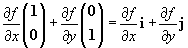
Ñf(x,y)= (2y³+2xy²)i+(4y³+6xy²+2x²y)j

Dus in het punt (0,1) is de richting van de gradiënt (2,4).
Uitgedrukt in i en j is dat 2i+4j.

Verder gaat het je om de 'rate of change' in de richting (1,2) (want
i+2j). Hiertoe moeten we deze richting eerst normeren op 1. Ofwel de vector (1,2) moeten we delen door de lengte ervan (door de absolute waarde van (1,2)). Daarom staat er bij jou (i+2j)/|i+2j|
|i+2j|=Ö(1²+2²)=Ö5
Hieruit volgt dus dat (i+2j)/|i+2j| =
(1/Ö5)i+(2/Ö5)j. dit is dus de vector (1/Ö5 , 2/Ö5)

Het inprodukt van (i+2j)/|i+2j| en (2i+4j) is dus (1/Ö5 , 2/Ö5)·(2,4) = 2/Ö5 + 8/Ö5 = 10/Ö5 = 2Ö5

groeten,

martijn

mg
30-1-2007