Er worden 500 studenten onderzocht, of ze lopen( L), fietsen(F) en/of zwemmen (Z).157 studenten doen geen van de drie sporten, 275 doen juist ¨¦¨¦n sport,61 juist twee sporten en 7 juist drie sporten.149 studenten lopen maar niet zwemmen, 162 lopen maar niet fietsen, 112 zwemmen maar niet lopen en dat er 128 zwemmen maar niet fietsen.
a) Hoeveel lopen, maar zwemmen en fietsen niet.opl=132
b) hoeveel studenten lopen en zwemmen, maar fietsen niet.opl=30
c) hoeveel lopen en fietsen, maar zwemmen niet?opl=17
500-157= 343 studenten doen minstens ¨¦¨¦n sport
Z U F U L= 343
L \ Z= 149
L \ F= 162
Z \ L= 112
Z \ F= 128
L ¡É F ¡É Z= 7
F \ L= 343 -(149+128+7)= 59
F \ Z= 343 -(162+112+7)= 62
En dan zit ik vast ik zie niet hoe je nu verder moet?Styn Hermans
13-12-2006
Ik zou het Venn-diagram maar 's tekenen:
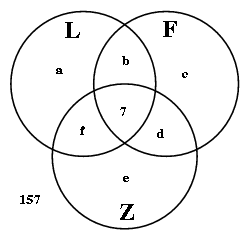
Als je de verschillende aantallen in de gebieden aangeeft met een variabele dan kan je de 'gegevens' vertalen naar een stelsel van 6 vergelijkingen met 6 onbekenden:
a+c+e=275
b+d+f=61
a+b=149
a+f=162
e+d=112
e+f=128
Oplossen en je weet alles!
WvR
13-12-2006
#48068 - Verzamelingen - Student Hoger Onderwijs België
