WisFaq!

Bewijzen dat het plastische getal 1,324718 is

Geachte meneer/mevrouw,

Dom van der Laan heeft het plastische getal bedacht. Er is een vergelijking voor. Breedte/lengte=lengte/hoogte=hoogte/(breedte+lengte)

Er is ook een plastische verhouding:

p²+p³=P⁵
P⁴+1=p⁵
P²+p+1=P⁵

En er is een meetkundige reeks:

1,p,p²,p³,p⁴,p⁵,p⁶ en p⁷

Of bij benadering: 1,4/3,7/3,3,4,21/4 en 7

Het plastische getal is 4/3 of 1,324718

Hoe komen ze aan het plastische getal? En kan je de andere verhoudingen dan ook afleiden, of is het dan gewoon de 4/3 in vullen in de rest van de reeks?

Bij de gulde snede is het mij wel gelukt om op 1.618 uit te komen. Dit is hetzelfde idee, maar dan in het platte vrak, in plaats van 3D.

Daar gebruikte ik de vergelijking breedte/lengte=lengte/(breedte+lengte)
De guldensnede verhouding is 1+p=p²

p²-1-p=0

abc formule gebruiken
En dan kom je op 1,618

Dat was niet zo moeilijk. Ik denk dat het met het plastisch getal net zo werkt. Maar bij de plastische verhoudingen gaat dat dus niet zo makkelijk. (Denk ik)

Ik hoop dat jullie kunnen laten zien dat het helemaal niet zo moeilijk is.

Rob Timmer
11-12-2006

Antwoord

Beste Rob,

Je hebt veel formules gevonden voor het plastisch getal. Met een van die formules, namelijk, p²+p³=p⁵, kun je de getalswaarde goed vinden. Als je deelt door p² krijg je immers 1+p=p³, dat is een derdegraadsformule die je met de Formule van Cardano op kunt lossen.

Met de formule in de link zie je dan dat het plastisch getal gelijk is aan:



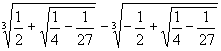
...en dat komt overeen met de afronding die je al gaf.

Zie MathWorld: Plastic Constant [http://mathworld.wolfram.com/PlasticConstant.html]

FvL
12-12-2006