WisFaq!

Algebraisch nulpunten bepalen van een functie met een parameter

Hallo,

Ik heb een vraag die luidt:
fc(x)=x³ + 3cx

a. Voor welke waarden van c heeft de grafiek drie nulpunten?
Ik weet dat je dan x buiten haakjes kan halen en dat je dan al 1 oplossing x=0 hebt, maar hoe moet je dan verder om de andere twee te vinden?

b Ook zou ik graag willen weten voor welke waarde van c fc een extremium van 4 heeft.

c. De laatste vraag is: Voor welke waarden van c heeft de lijn met vergelijking y=x precies één punt met de grafiek van fc gemeen?

Dit moet allemaal algebraisch..
Ik hoop dat u mij kunt helpen, want ik heb donderdag een toets en ik kom er niet uit. Kunt u de vragen in het Nederlands beantwoorden?

Groeten, Nienke

Nienke
9-12-2006

Antwoord

Hallo Nienke,

a.

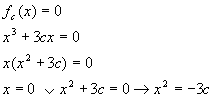
Er zijn 3 oplossingen als x² = -3c twee oplossingen heeft.
Dit kan alleen als -3c 0 ® c 0

b.
Punt (x,4) is een top als geldt dat :


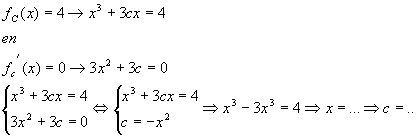
c.


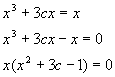
Hier van is x = 0 een van de oplossingen.
Als dit de enige oplossing is dan moet voor x² + 3c -1 =0 ook gelden dat
x = 0 de enige oplossing is.

wl
9-12-2006