WisFaq!

Kortste afstand tussen twee punten op een kegel

Een rechte cirkelvormige kegel is 20 cm hoog met een straal van de basis gelijk aan 10cm. Een kever start in een punt S, 5 cm onder de top T tot een punt F, 12 cm onder T, aan de andere kant (met andere woorden TS en TF snijden de basis in diametraal tegenovergestelde punten). Wat is de kortste afstand die de kever moet afleggen?

Linda Nieman
25-11-2006

Antwoord

hier zien we de kegel in 3-D

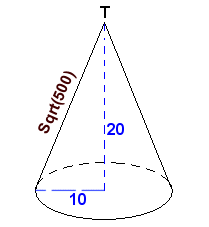
De hoogte is 20, en de straal van de basis is 10, dus mbv Pythagoras is de afstand van top naar basis (de schuine zijde zeg maar) gelijk aan Ö500.

Om het vraagstuk op te kunnen lossen, moeten we in gedachten de kegel openknippen langs zo'n schuine zijde, en dan uitvouwen/platmaken.

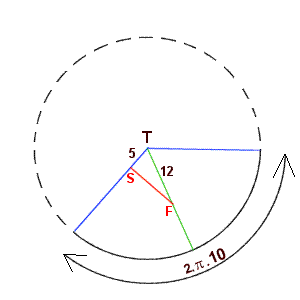
We zien dan de kegelmantel eigenlijk een onderdeel is van een cirkel.
De schuine zijde van de kegelmantel (Ö500) vormt de straal van de grote cirkel.
Verder was de straal van de basis van de kegel 10, dus de cirkelvormige basis van de kegel had een omtrek van 2p10.
Dit is nu het cirkelsegment geworden van de grote cirkel.

S ligt 5 cm onder T, en F 12 cm onder T, diametraal tegenover. Als we dat op de uitgevouwen cilindermantel uitzetten, moet F op de groene lijn liggen welke de bissectrice vormt van het cirkelsegment.
Die booglengte van dat halve cirkelsegment is de helft van 2p10, ofwel deze is gelijk aan 10p.

Tot slot vormt TSF een driehoek bestaande uit louter rechte lijnen. Je wilt uiteindelijk de lengte weten van SF.
Hiervoor roepen we de cosinusregel in herinnering:
a²=b²+c²-2bc.cosa
Wanneer we dit toepassen op de driehoek in kwestie, is SF de onbekende lengte a, zijn b en c de lengtes van TS en TF, en is a de hoek STF

Hoe kom je nou aan a? Wel, a is een *gedeelte* van de grote cirkel, en is dus een gedeelte van 2p (gedeelte van de 'volle omtrek')
De volle omtrek van de grote cirkel heeft een lengte 2pÖ500 en het cirkelsegment waar a bij hoort, heeft lengte 10p.
Dus a=fractie*2p = (10p/2pÖ500)*2p = p/Ö5

Nu kun je SF uitrekenen.

groeten,
martijn

mg
25-11-2006