WisFaq!

Inhoud van een kegel

hallo. ik ben op de volgende, volgens mij, redelijk lastige vraag gestuit...

Een rechte kegel heeft een hoogte h en een grondcirkel met straal r.
Leid met behulp van integreren een formule af voor de inhoud van deze kegel.

de punt van de kegel zit in de oorsprong en de hoogtelijn loopt gelijk aan de x-as.

dit betekent dat je deze vraag kunt oplossen met behulp van de omwentelingslichamen rond de x-as, maar ik heb geen flauw idee waar ik moet beginnen...

alvast bedankt...

Carel
17-10-2006

Antwoord

Een kegel kun je vormen uit het omwentelingslichaam van een rechte lijn.
De top van de kegel bevindt zich in de oorsprong dus de lijn moet ook door de oorsprong lopen.
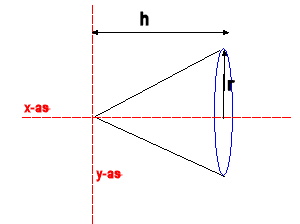
Verder weet je dat de hoogte van de kegel gelijk is aan h, en dat de straal van het grondvlak gelijk is aan r.
Aan het plaatje kun je zien wat de situatie is en waar h en r zitten.
Je weet dus 2 dingen nu van de lijn in kwestie:
a. hij loopt door de oorsprong;
b. hij heeft een richtingscoëfficiënt van r/h

de vergelijking van de lijn is dus y=(r/h).x

Berekening van de inhoud van het omwentelingslichaam:

I= pòy²dx (grenzen van 0 tot h)
= ... (reken zelf na!)
= ¹/₃.p.r².h
= ¹/₃.grondvlak.hoogte

groeten,

martijn

mg
17-10-2006