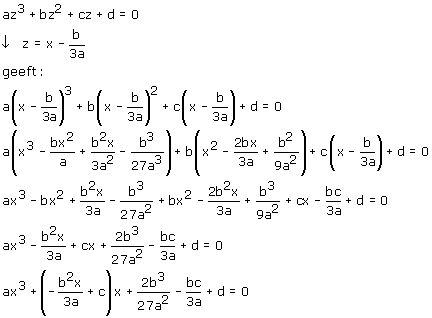WisFaq!

Verbanden bij vergelijkingen

Hallo,

Ik heb een paar vraagjes:

deze vraag gaat over de volgende opdracht.
4x⁴+3x³-2x²+3x+4=0
Ik heb al gezien dat de uitwerking van deze vraag elders op de site staat. Deze is mij nog niet geheel duidelijk, maar ik zal zo nog een blik werpen.

Mijn vraag is echter niet om de uitwerking of het antwoord, maar of er duidelijk verbanden bestaan bij het oplossen van vergelijkingen. Met betrekking tot deze: het viel mij op dat er gebruik gemaakt wordt van 4x⁴, 3x³ en 2x². Is dat toeval dat het grondtal en de exponent met elkaar corresponderen?

Ook vroeg ik mij af.. ik heb geprobeerd jullie divers uitleggen te volgen over de methode van cardano. Maar met het subsitieren van z=x-b/3a en het vereenvoudigen, kwam ik uit op x³-bx²/a+b²/3a²x-b³/27a³ en niet op
/ b² \ b³ c b
V := a x3 + |- 1/3 ---- + c| x + 2/27 -- + d - 1/3 --- = 0
\ a / a² a

die /27 en b³/a.
Ik heb t twee keer nagerekend en beide keren kwam ik uit op op mijn bovenstaand antwoord. Ik heb (x)³ opgelost door (x)²(x) te doen. Dat is toch correct?

mijn laatste vraag: ik probeer nu de vergelijking 6x³-7x²-16x+12=0 op te lossen.
Door 6x³-7x²-16x=-12 kom ik niet verder. Het is dan vervolgens te delen door x, maar dit zou een discriminatie opleveren 0. Dus ook daar kom ik niet verder mee. Naar mijn idee is dit hetzelfde probleem als de opdracht hierboven. Zoniet... kunt u mij een eindje opweg helpen?
Kun u mij vertellen waar ik de mist in ga, of welke denkstap ik over het hoofd zie?

bij voorbaat dank!

Lien
24-8-2006

Antwoord

1.
Is dat toeval dat het grondtal en de exponent met elkaar corresponderen?

Ja.. en toch niet... je kunt proberen of x=-1 of x=1 'toevallig' een oplossing is. Zo ja, dan kan je ontbinden in factoren! In dit geval blijkt dat te gaan want x=-1 is oplossing dus ontbinden met (x+1).

2.
Dit gaat over Formule van Cardano. Subsitutie levert:



Dus dat klopt wel... maar wat je verder bedoelt met die '(x²)x' is me niet duidelijk.

3.
Om een derdegraads vergelijking op te lossen kan je eerst eens kijken of er niet 'snel' een oplossing te vinden is door te proberen of x=1, x=-1, x=2 misschien oplossingen zijn... (gebruik eventueel je GR om zo'n oplossing te vinden).

In dit geval is x=2 oplossing dus kan je ontbinden met x-2. Je krijgt dan iets van de vorm (x-2)(...)=0 waarbij er op de puntjes een tweedegraads vergelijking staat... en die kan je wel oplossen waarschijnlijk.
Zie 2. Tweedegraads vergelijkingen oplossen

WvR
24-8-2006