Nee, dat doe je niet goed, hoewel het antwoord 1 wel klopt.
Je vervangt eerst 1/n door x, zoals je dat ook deed bij de opgaven daarvoor.
Omdat n naar ¥ gaat, betekent dit: x gaat naar 0.
n·sin(1/n) = 1/x·sin(x) = sin(x)/x
Je krijgt dus als limiet:
limx¯0 sin(x)/x·limn®¥ n/n-3
De eerste van deze twee limieten is gelijk aan 1, en de tweede ook, maar dat moet je weer op een andere manier aantonen, zoals je bij je eerste opgave deed.
Dan die logaritme.
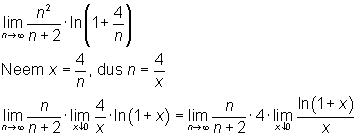
Lukt dat verder? Succes,
Anneke
16-8-2006