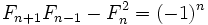
Op Cassini's identity kan je daar een bewijs voor vinden. Misschien kan je aan dat bewijs een beetje inschatten of je 't allemaal nog haalt voor morgen...
WvR
23-5-2006
Beste wisfaq,
Ik heb iets leuks bij de lucasrij gezien namelijk:
bij de volgende (2,9,11,20,31,51,82,133) geldt
Waneer we een getal uit de rij kwadrateren en vervolgens dat kwadraat verminderen met het voorgaande getal vermenigvuldigd met de opvolger van het getal dat je kwadrateert dan komt er een constant getal uit dat steeds wisselt van positief en negatief.
(20·20)-(11·31)=59
(31·31)-(20·51)=-59
59 is de constante en is om en om positief en negatief
-Hoe moet je dit bewijzen?
-En is dit ook bij andere rijen of wiskundige aspecten het geval, zo ja waar?
SVP zo snel mogelijk antwoord want ik moet het morgen inleveren.
Alvast bedankt!
Piet
23-5-2006
Er bestaat een vergelijkbare stelling voor de rij van Fibonacci:
Op Cassini's identity kan je daar een bewijs voor vinden. Misschien kan je aan dat bewijs een beetje inschatten of je 't allemaal nog haalt voor morgen...
WvR
23-5-2006
#45538 - Fibonacci en gulden snede - Leerling bovenbouw havo-vwo