WisFaq!

Standaardafwijking berekenen bij een normaalverdeling

Ik oefen nu een examen van 2005 wiskunde b1 alleen ik echt niet uit een vraag:

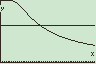
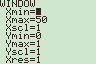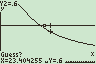
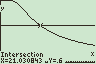
De normale verdeling van het aantal sterfgevallen per dag in Nederland heeft een gemiddelde van 385. Een grafiek hiervan staat hiernaast.
Gegeven is dat de kans op een uitkomst tussen 367,3 en 402,7 bij deze normale verdeling 60% is. Zie daarvoor de figuur en het grijs gekleurde vlakdeel.

• Bereken de standaardafwijking van deze verdeling.

Ik snap er niks van...

kris
15-5-2006

Antwoord

Het probleem van deze opgave is dat er geen 'directe' manier is om met je GR de standaarddeviatie uit te rekenen bij een gegeven gemiddelde, grenzen en oppervlakte.

Maar je kan een truuk uithalen. Ik zet in Y1 de functie:

Y1=normalcdf(367.3,402.7,385,X)

Hierin is X de gevraagde standaarddeviatie en bij een bepaalde waarde van X moet Y1 gelijk zijn aan 0,6.

Y2=0.6

Als ik nu Y1 en Y2 ga plotten en het snijpunt kan bepalen, dan ben ik er uit.













..en dat gaat prima.

Tweede methode
Een andere methode is gebruik maken van de standaard normale verdeling. Op Werken met de normale verdeling kan je daar een uitleg over vinden. Zie ook De standaardafwijking berekenen met de rekenmachine.

WvR
15-5-2006