In bijgevoegde figuur vind je mijn denkpiste...
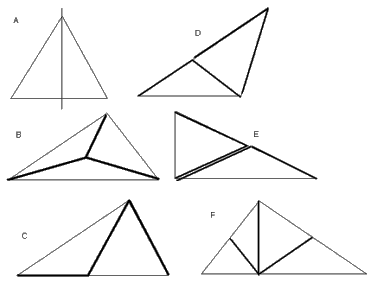
In figuur A hebben we een gelijkbenige driehoek. Dit is het eenvoudige geval.
Daarna probeerde ik een driehoek in gelijkbenige driehoeken te verdelen. Voor een scherphoekige driehoek kan dit met behulp van het middelpunt van de omgeschreven cirkel (figuur B). Door 2 van de 3 driehoeken van plaats te wisselen krijgen we een inversie.
Voor een rechthoekige driehoek hebben we de situatie zoals figuur E (middelpunt van omgeschreven cirkel in midden van schuine zijde). Door één van de twee driehoeken te draaien rond dit midden totdat hij met zijn ander been vastklikt, inverteren we de driehoek.
Terloops ontdekte ik ook wat speciale gevallen zoals in figuren C en D. Je kan de voorwaarden voor de hoeken hiervan makkelijk afleiden. Ze zijn op het eerste zicht niet te veralgemenen.
Voor een stomphoekige driehoek had ik nog geen oplossing. In figuur F heb ik de loodlijn uit de tophoek neergelaten en het basispunt met de middens van de opstaande zijden verbonden. Met 3 sneden hebben we 4 driehoeken die samen 2 rechthoekige vormen. Hierboven staat hoe we elk kunnen inverteren. Als we ze weer samenvoegen volgens de hoogtelijn, dan hebben we de hele driehoek geïnverteerd. Let wel dat we in dit geval op 4 driehoeken komen. Voor scherphoekige driehoeken vonden we eigenlijk beter: in 3 driehoeken (maar ook met 3 sneden).
Wellicht kan je hier al een eind mee op weg. De volledige uitwerking laat ik aan jou.
Groetjes,
Johan
andros
30-9-2002