WisFaq!

Raaklijnen met e

Gegeven zijn de functies f(x) = e^x-3 en g(x) = e²x+p (lineaire functie)

1. voor welke p heeft de vergelijking f(x)=g(x) geen oplossingen?

Door het punt (2,0) gaan twee raaklijnen aan de grafiek van f. Deze raaklijnen raken de grafiek van f in de punten P en Q.

2. bereken de afstand tussen P en Q in 2 decimalen nauwkeurig.

Groetjes

kim
21-4-2006

Antwoord

a)

De richtingscoefficient van de rechte lijn is e^2.
Als je p zo kiest dat de rechte lijn de raaklijn is aan de grafiek van f in het punt met x=2 dan heeft deze lijn precies 1 punt gemeen met de grafiek van f.
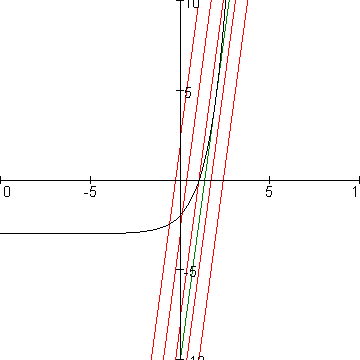
In bovenstaand plaatje heb ik in groen de raaklijn aan de grafiek van f in (2,f(2)) getekend en in rood een aantal lijnen evenwijdig aan die raaklijn.
We stellen de vergelijking van de raaklijn in (2,f(2)) op:
y=e²(x-2)+e²-3
dus
y=e²x-2e²+e²-3
y=e²x-e²-3
Als we p kleiner kiezen dan -e²-3 heeft de grafiek van g(x) dus geen punten gemeen met de grafiek van f.

2)
Voor P en voor Q geldt dat de raaklijn in dit punt door het punt (2,0) moet gaan.
De raaklijn in een willekeurig punt (p,f(p)) heeft als vergelijking
y=e^p(x-p)+e^p-3
Invullen van x=2 en y=0 levert
e^p(2-p)+e^p-3=0.
De oplossingen van deze vergelijking zijn de x-coordinaten van P en Q.
Deze vergelijking kun je het beste oplossen met je GRM.
Vervolgens bereken je ook de y-coordinaten van P en van Q en de afstand.

groetjes

hk
21-4-2006