WisFaq!

Foutfunctie

Hoi,
Ik heb een probleem. Ik moet het volgende aantonen:
Je hebt vierkant S=[-a,a]^2
Toon aan dat met behulp van poolcoordinaten de dubbele integraal overgaat in een enkele integraal:
òò(over S) e^(-x^2-y^2)dxdy = 4 ò(0 naar p/4) (1-e^((-a^2)/cos^2(q)))dq

Hoe toon ik dit aan?

Heel erg bedankt,
Luc

Luc
18-4-2006

Antwoord

Beste Luc,

Zoals je aan de grenzen van de hoek kan zien gaan we integreren over één achtste van het vierkant. Om de volledige oppervlakte te hebben moeten we dus vermenigvuldigen met 8. Naast de hoek hebben we bij poolcoördinaten de straal r: deze moet lopen van 0 tot aan de rechterzijkant van het vierkant. Dit heeft als vergelijking x = a, maar in poolcoördinaten is x = r.cos(t) zodat: r.cos(t) = a Û r = a/cos(t). Dus; r loopt van 0 tot a/cos(t). Vergeet tenslotte niet dat dxdy overgaat in rdrdt, zodat we krijgen:



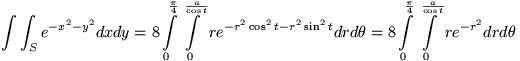
Dit kan je nu integreren naar r, als het goed is vind je dan de opgegeven integraal in theta.

mvg,
Tom

td
18-4-2006