WisFaq!

Leukste raadsel sinds maanden

Van een even getal is de som van de cijfers 95; de som van de cijfers van de helft van dat getal is 70. Hoeveel oneven cijfers heeft dat getal?
Ik moet deze vraag beantwoorden, hopelijk kunnen jullie me op de weg helpen, want ik heb echt geen idee hoe ik dit probleem zou moeten oplossen.

Bij voorbaat dank

ramonageers
24-9-2002

Antwoord

Waaw... leukste raadsel sinds maanden...

Here we go:
Het even getal uit de opgave stellen voor door 2n.
Er zijn c_i cijfers i in een getal n.

We onderzoeken wat er precies gebeurt wanneer we met 2 vermenigvuldigen:



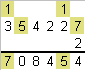
We zien:
- cijfers 5,6,7,8 en 9 in n leiden tot oneven cijfers in 2n
- cijfers 0,1,2,3 en 4 in n leiden tot even cijfers in 2n
- een cijfer 0 in n geeft een bijdrage 0 in de som der cijfers van 2n
- een cijfer 1 in n geeft een bijdrage 2 in de som der cijfers van 2n
- een cijfer 2 in n geeft een bijdrage 4 in de som der cijfers van 2n
- een cijfer 3 in n geeft een bijdrage 6 in de som der cijfers van 2n
- een cijfer 4 in n geeft een bijdrage 8 in de som der cijfers van 2n
- een cijfer 5 in n geeft een bijdrage 1+0=1 in de som der cijfers van 2n
- een cijfer 6 in n geeft een bijdrage 1+2=3 in de som der cijfers van 2n
- een cijfer 7 in n geeft een bijdrage 1+4=5 in de som der cijfers van 2n
- een cijfer 8 in n geeft een bijdrage 1+6=7 in de som der cijfers van 2n
- een cijfer 9 in n geeft een bijdrage 1+8=9 in de som der cijfers van 2n

Dus:
0.c₀+1.c₁+2.c₂+3.c₃+4.c₄+5.c₅+6.c₆+7.c₇+8.c₈+9.c₉=70 (1)

en

0.c₀+2.c₁+4.c₂+6.c₃+8.c₄+1.c₅+3.c₆+5.c₇+7.c₈+9.c₉=95 (2)

2.(1)-(2):
9.c₅+9.c₆+9.c₇+9.c₈+9.c₉=2.70-95
en dus: c₅+c₆+c₇+c₈+c₉=5.
Of: het aantal cijfers 5,6,7,8 of 9 in n is 5. Dit zijn de enige cijfers die oneven cijfers in 2n veroorzaken. In 2n zijn er dus 5 oneven cijfers...

Groetjes,
Johan

andros
24-9-2002