WisFaq!

De grootste inhoud

Uit een stuk aluminium papier van 13 bij 13 (169cm²) moet ik een simpel bootje maken met de meeste inhoud. Deze afmetingen liggen dus ergens bij de 9x9x2 cm. Maar niet precies! Hoe kan ik deze toch precies vinden?

Ik moet er dus voor zorgen dat het bootje de meeste inhoud heeft (met behulp van de afgeleiden?). Als de afgeleide van de functie bij een bepaalde waarde 0 is, dan is de functie maximaal. Hoe moet ik dit aanpakken?

gea nigten
9-2-2006

Antwoord

Dit is wel aardig... tenminste als je bedoelt dat het bootje de vorm moet krijgen van een doosje zonder deksel met van de hoeken van het vierkant uitgeknipte vierkantjes... tekening dan maar?



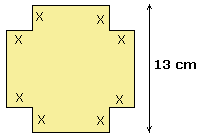
Je kunt dan de inhoud uitdrukken in 'x'. De formule daarvoor is:

I(x)=x·(13-2x)²

Voor het maximaliseren bereken je de afgeleide:

I'(x)=1·(13-2x)²+x·2(13-2x)·-2

(Productregel en kettingregel!)

I'(x)=(13-2x)²-4x(13-2x)=(13-2x)·(13-2x-4x)=(13-2x)·(13-6x)

Als je nu I'(x)=0 neemt vindt je twee waarden voor x:

x=6¹/₂ (weinig doosje meer...) of x=2¹/₆.

Daarmee zouden de afmetingen van het doosje neerkomen op 8²/₃ en 2¹/₆. Dus inderdaad met de afgeleide...

Zie ook Een doosje van een vierkant stuk karton en 3. Optimaliseringsproblemen.

Maar... eh dat is wel 'toevallig' de lengte en breedte zijn precies 4 keer zo groot als de hoogte... of zou dat geen toeval zijn?

WvR
9-2-2006