WisFaq!

Yahtzee: kleine straat

Wat is de kans dat je een kleine straat gooit in 1 worp.
Met de hulp van deze site was ik tot dit punt gekomen:
er zijn 3 mogelijke kleine straten 1234, 2345, 3456
elke mogelijke kleine straat kan op 4! manieren geschreven worden en omdat je met dobbelstenen gooit is er op elke manier dus een kans van:
3*4!*(1/6)^4
Nu blijf ik alleen nog zitten dat je met 5 dobbelstenen gooit in plaats van met 4 dus... hoe verder??

Jimmy
16-9-2002

Antwoord

Hoi,

Ik denk dat je best zolang mogelijk wacht om in 'kansen' te rekenen. Je heb zo een beter zich op hoe je dubbele tellingen (12345, ...) kan vermijden.
Het is ook eenvoudiger tellen als we de dobbelstenen nummeren en een volgorde in de geworpen nummers krijgen.

Mogelijke worpen: n= 6⁵
Mogelijk goeie worpen:
A: bevat 1234
B: bevat 2345
C: bevat 3456
Je kan deze als Venn-diagram voorstellen.



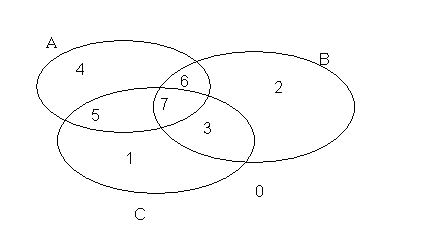
We berekenen het aantal worpen in elk gebied:
G5=G7=0
G4=5!+4.5.4!/2 (5 aanvullingen mogelijk: 1,2,3,4 of 6. Voor 6 hebben we 5! mogelijkheden. Voor andere hebben we 4! mogelijkheden voor 1,2,3,4 en 5 plaatsen om een dubbel in te voegen; deze werden dan wel allemaal dubbel geteld, vandaar de extra 2)
G1=G4
G6=5! (geen aanvullingen mogelijk)
G3=G6
G2=4.5.4!/2 (4 aanvullingen mogelijk: alles behalve 1 en 6; dubbels weggedeeld)
G0=n-G1-G2-...-G7

Het aantal worpen in G1, G2 en G4 samen noemen we m (Grote Straten in G3 en G6).
De kans is dus m/n=8.5!/6⁵@12.3%...

Groetjes,

Johan

andros
17-9-2002