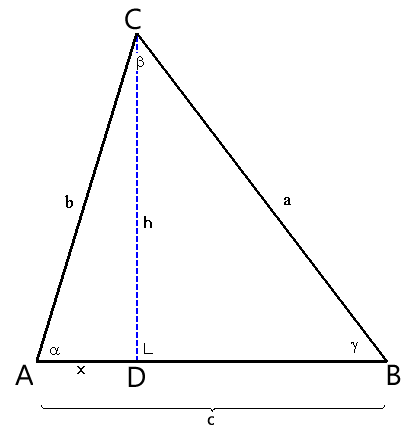
We stellen vast:
x=bĚcosa
h=bĚsina
x2+h2=
(bĚcosa)2+(bĚsina)2=
b2Ěcos2a+b2Ěsin2a=
b2(cos2a+sin2a)=
b2
-2cx=-2cĚbĚcosa=-2bcĚcosa
Waarmee we volgens mij helemaal rond zijn...
WvR
29-1-2006
Hallo,
Mijn vraag gaat over de cosinusregel.
Ik heb een scherpe driehoek ABC en een hoogtelijn vanuit C
met voetpunt D. (CD)=h
waarvan ad=x en bd =(c-x)
te bewijzen a2 = b2+ c2-2bccosalfa
a2=(c-x)2 + h2 =c2 - 2cx + x2 + h2
en b2= x2+ h2
dus a2+ b2-2cx waarbij x2+ h2 vervangen is door b2.
ik hoop dat ik dit goed begrijp.
Dat-2cx vervangen wordt door -2bccosalfa snap ik niet.
bĚcosalfa = lengte x. snap ik.
hier kom ik niet verder.
BVD
Mari Steffek
29-1-2006
We stellen vast:
x=bĚcosa
h=bĚsina
x2+h2=
(bĚcosa)2+(bĚsina)2=
b2Ěcos2a+b2Ěsin2a=
b2(cos2a+sin2a)=
b2
-2cx=-2cĚbĚcosa=-2bcĚcosa
Waarmee we volgens mij helemaal rond zijn...
WvR
29-1-2006
#43359 - Goniometrie - Ouder