Op vraag van collega pl zal ik proberen je vraag grafisch te illustreren.
Eerst teken je de twee lijnen (teken twee punten van elke lijn, trek de lijn door de punten - moest je dat nog niet weten). We krijgen dan 3x+2y=3 (in het blauw) en x+y=0 (in het rood)
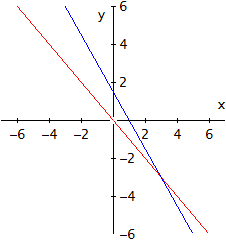
Beide lijnen delen het vlak nu in twee delen. Elke ongelijkheid stelt dan een helft van het vlak voor, aan één van beide kanten van de lijn. Om te weten welke kan je voor elke lijn een punt nemen dat niet op de lijn ligt en kijken of het aan de ongelijkheid voldoet. Zoja: dan ligt het punt in de juiste helft, zonee: dan is het de andere helft.
Voor de rode lijn kan je testen met het punt (1,1), deze voldoet aan de ongelijkheid dus we vinden het volgende groene gebied dat met de ongelijkheid overeenstemt.
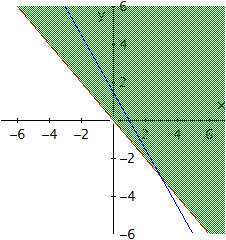
Op dezelfde manier kunnen we het punt (1,1) in de andere ongelijkheid steken. Dit blijkt niet te kloppen, dus het gebied dat we zoeken ligt aan de andere kant van de blauwe lijn, dus het gebied waar (1,1) niet in ligt; in het geel.
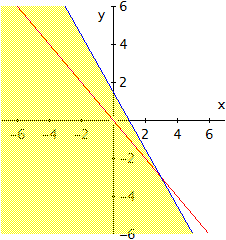
Een stelsel van ongelijkheden legt nu gewoon op dat aan beide ongelijkheden voldaan moet zijn. We zoeken dus het gebied waar de vorige twee gebieden overlappen, dat ziet er dan zo uit, in het rood.
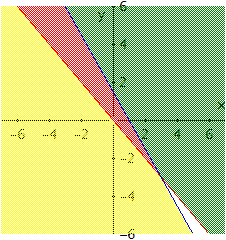
De punten die enkel aan één van beide ongelijkheden voldoen maar niet aan de andere zijn geen oplossing van het stelsel, dus de uiteindelijke oplossing is enkel het rode overlappingsgebied, hier afgebeeld.
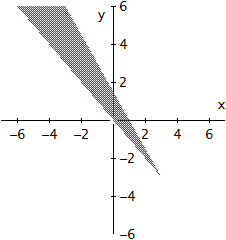
Hopelijk duidelijk zo

mvg,
Tom
td
17-1-2006