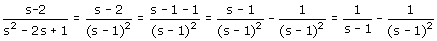Ik zit met een probleem.
Ik ben bezig met de opgave (en heb de uitwerking er ook van):
y''-2y+y=step(t,1)
Eerst de laplace getransformeerde hiervan (dat is een kwestie van de formules toepassen) en dan krijg je dit:
s2L[y]s-s-2sL[y]s+2+L[y]s = e^-s/s
=
(s2-2s+1)L[y]s-s+2 = e^-s/s =
(s2-2s+1)L[y]s = s-2 + e^-s/s =
L[y]s= s-2/(s2-s+1)+ e^-s/s(s2-2s+1) =
L[y]s= s-2/(s-1)2 +e^-s/s(s-1)2 =
L[y]s= s-1-1/(s-1)2 + e^-s/s(s-1)2 Nu geeft de docent de volgende stap en dat is dus wat mij onduidelijk is :
L[y]s= 1/(s-1) - 1/(s-1)2 +e^-s/s(s-1)2
Ik snap dus niet waar ze die 1/s-1 opeens vandaan haalt...
Kan iemand mij misschien helpen?? (heel graag!!)
thank you!!
Mvg,
N
11-1-2006
