WisFaq!

Exponentiel trigon0metrische functie

Bereken voor x$\to$0 van lim sin(x)^tg(x): (volgens de opgave = 1)

D1t is onbepaalde limiet 0⁰ dus gebruik ik de formule lim e^tg(x).ln(sin(x)) , dit is nu lim e^tg(x).lim e ^ln(sin(x))
de 1ste lim geeft voor x $\to$0 : e⁰ = 1 en de tweede lim kan gelijkgesteld worden aan de lim sin(x)= 0 dus 1.0 = 0 . Waar ligt mijn fout vermits het antwoord 1 moet zijn ?

J-P.
3-1-2006

Antwoord

Beste Jean-Pierre,

De fout zit waar je je limiet splitst in het product van twee limieten. Er geldt namelijk wel dat e^(a+b) = e^a.e^b maar er staat hier geen som maar een product als exponent. Wat je wel kan doen is de limiet naar de exponent brengen.



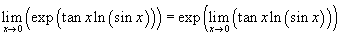
Nu heb je het herleid naar de onbepaaldheid 0.(-¥) en deze is in één stap te herleiden naar een onbepaaldheid van de vorm 0/0 of ¥/¥ waar je L'Hopital op mag toepassen. Doe dit door f(x)g(x) te schrijven als g(x)/(1/f(x)).

mvg,
Tom

td
3-1-2006