WisFaq!

Bewijs dat 3 punten op een lijn liggen

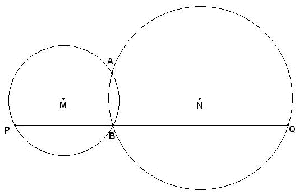
Je hebt 2 cirkels die elkaar snijden in de punten A en B. De snijpunten worden in middelpunt M respectievelijk middelpunt N gespiegeld. Deze punten worden P en Q genoemd. Hoe bewijs je dat PQ altijd op 1 lijn ligt met punt B?



Alvast bedankt

Jules Holleboom
20-12-2005

Antwoord

Een manier om te bewijzen dat een punt B op een lijn PQ ligt is dat je aantoont dat ÐPBQ gestrekt is, dus 180° is.

Het middelpunt M van de linkercirkel ligt op AP, dus AP is een middellijn van de linker cirkel. B ligt op deze cirkel dus geldt volgens de omgekeerde stelling van Thales ÐPBA=90°.
Analoog geldt ÐQBA=90°. Dus ÐPBQ=180°.
Dus ligt B op lijnstuk PQ.

hk
20-12-2005