Niet zo'n eenvoudig opgaafje!
We hebben dus 14 horizontale en 19 verticale banen. Als we een aantal horizontale en een aantal verticale banen naast elkaar kiezen, dan bepalen die de lengte en breedte van een rechthoek. En zo kunnen we elke rechthoek vinden.
Nu kunnen we dit keuzeproces coderen met 0 en 1. Dan symboliseert een 0 een baan en een 1 een overgang van niet naar wel gekozen en andersom. Voor de horizontale banen komt dat dus neer op veertien 0-en en twee 1-en. De keuze voor de middelste vier banen staat gecodeerd in 0000010000100000:
We zouden ons probleem dan dus vereenvoudigen tot het kiezen rijtjes van 14 nullen en 2 enen. Helaas is er een addertje onder het gras. Want twee enen na elkaar, dat zou een rechthoek zonder breedte opleveren! Dat mag natuurlijk niet. Dus moeten we een kleine aanpassing maken: de eerste 1 symboliseert behalve een overgang van niet naar wel gekozen tegelijk ook de eerste gekozen baan. Het rijtje voor de middelste vier banen is nu dus gecodeerd in 000001000100000.
Okay, We zijn dus gekomen tot een rijtje van vijftien getallen, waarvan dertien nullen en twee enen. Op hoeveel manieren kan dat gedaan? Het komt neer op het kiezen van twee enen tussen vijftien getallen (de rest wordt nul). Dat gaat op
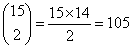manieren.Evenzo vinden we dat de verticale banen op 20×19/2=190 manieren kunnen worden gekozen.
Even vermenigvuldigen, and you are done.
***
Tja, dan heb je zo'n mooi verhaal met coderingen bedacht. Het kan veel simpeler! Van de 15 horizontale lijnen moet je er twee hebben die de grenzen vormen van de horizontale banen die we moeten hebben. Dat is op veel simpeler manier een keuze van 2 uit vijftien.
Het coderingsverhaal is wel mooier!
FvL
7-12-2005