Ik was bezig met het berekenen van de convergentiesnelheid van 2 rijen. De oplossing in -8/3 maar bij de uitwerking loop zit ik vast. Ik weet dat je bij limietberekening naar oneindig de hoogstegraadtermen moet nemen, maar kan deze niet goed terugvinden.
de rij x1 = {n-1/n+3}
en rij x2 = {√n+4/√n+1}
Ik zoek nu limn®$\infty$ x1 -1/x2 -1 Na elke tussenstappen bekom ik
limn®$\infty$ -4√n+1(n+3)(√(n+4)-√(n+1) Maar hier zit ik helaas vast, misschien een klein tip voor mij?Mohamed
16-11-2005
Beste Mohamed,
Het is eerst wat algebraïsch rekenwerk om te vereenvoudigen.
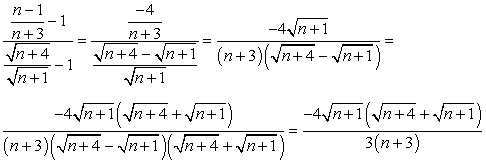
Ik heb eerst de breuken wat vereenvoudigd en daarna de noemer wortel-vrij gemaakt door met de toegevoegde uitdrukking van dat verschil van vierkantswortels te vermenigvuldigen, in teller en noemer.
Let nu goed op, de hoogste macht lijkt misschien n in de noemer maar het product van √n met een andere √n geeft ook iets van graad 1, en dat komt twee keer in de teller voor! Zie je hoe je aan -8/3 komt?
mvg,
Tom
td
16-11-2005
#41593 - Limieten - 3de graad ASO