WisFaq!

Iso-afstandslijnen

Gegevens is een willekeurige vierhoek ABCD met |AB| = 6, |BC| = 4, |CD| = 7 en |AD| = 5. ÐB is recht, ÐA en ÐC zijn stomp en ÐD is scherp. (Exacte maten zijn onbekend; ik heb een schets gemaakt. De docent legde uit, dat wanneer je bij dit figuur de iso-2-lijn tekent, de bogen bij de hoekpunten samen een hele cirkel vormen. Ik vraag me af of dit toeval is of niet. Mijn vraag is dus eigenlijk: Wanneer je bij een willekeurige vierhoek (zonder inkeping) een iso-afstandslijn
moet tekenen, vormen dan de vier bogen bij de hoekpunten ALTIJD samen een
hele cirkel? Zo ja, is dat ook te bewijzen?

Bedankt alvast voor het antwoord!

Wilma
5-11-2005

Antwoord

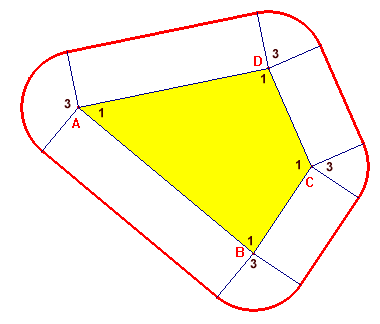
Ik denk 't wel. Kijk maar 's naar deze tekening:



Kun je nu 'bewijzen' dat: ÐA₃+ÐB₃+ÐC₃+ÐD₃=360°?

Vast wel...

WvR
5-11-2005