WisFaq!

Re: Integraal berekenen

Schets :



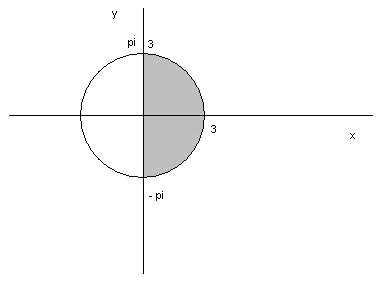
Grenzen in poolcoordinaten:

x = r.cos(t)
y = r.sin(t)

0 r 3 -p (t) p

Integraal berekenen:

ò₀³ò_-p^p1/_{Ö(r².cos²(t) + r².sin²(t)} drdt

cos2(t) = 1 - 2sin²(t)
sin2(t) = 2sin(t)cos(t)

Kunt u voor mij dit verder afmaken, want dan kan ik dit als voorbeeld gebruiken voor de rest van de sommen die ik nog heb.

vriendelijk bedankt.
mvg maarten

Maarten
23-10-2005

Antwoord

Beste Maarten,

Je schets is correct maar ik denk wel dat t dan loopt van -p/2 tot p/2, en niet van -p tot p (dat zou een hele cirkel zijn!).

Verder ben je vergeten dat dxdy overgaat naar poolcoördinaten volgens rdrdt, vergeet de extra r niet!

Ten slotte wordt de noemer zeer eenvoudig als je je de hoofdformule van de goniometrie herinnert: cos²x + sin²x = 1, dus breng de factor r² gewoon buiten haakjes en binnenin wordt het 1.

mvg,
Tom

td
24-10-2005