WisFaq!

Re: Primitieve functie

Mijn excuses voor mijn onduidelijkheid: ik vraag me dus af hoe je bewijst dat F(b)-F(a)=de integraal van de functie f voor het interval [a,b] (uw eerste gelijkheid).

Sebastian
5-10-2005

Antwoord

Dat kan, ik zal er dan wel (ongeveer) het tweede voor gebruiken.
Ik zal het bewijs in grote lijnen uiteenzetten, achteraf verwijs ik dan naar bronnen waar je andere (uitgebreidere) bewijzen kan vinden.

We beginnen met een continue functie f en (volgens de eerder gegeven definitie), een primitieve functie F. We willen dan bewijzen dat



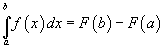
We beschouwen een continue functie g



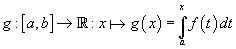
We nemen g ook afleidbaar en hebben dan dat



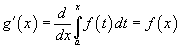
Ik veronderstel dat dit geldt, in principe kan je ook dit gaan bewijzen. Dat kan door gebruik te maken van de stelling van het gemiddelde. Het is niet zo moeilijk maar dat laat ik hier achterwege.

Dus g'(x) = F'(x) = f(x) maar dit impliceert dat er een constante c bestaat zodat g(x) = F(x) + c (*)

Stellen we nu in onze functie g x = a, dan vinden we



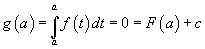
Zodat c = -F(a) en dus g(x) = F(x) - F(a) (zie (*))

Als we nu tenslotte x = b stellen als grens, dan volgt de stelling

Op onderstaande (Engelstalige) link vind je twee volledig andere bewijzen die niet gebruik maken van de hulpfunctie g. Ze zijn dan ook wat langer maar wel wat 'fundamenteler'.

Wikipedia: Fundamental theorem of calculus

mvg,
Tom

td
6-10-2005