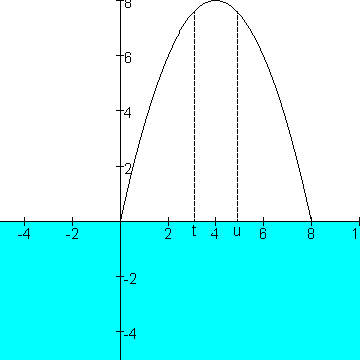
Ik heb twee verticale lijnen aangegeven die als grens tussen de gebieden zouden kunnen gelden.
Er zou dan moeten gelden 0òtydx=1/3*0ò8ydx en uò8ydx=1/3*0ò8ydx.
hk
5-10-2005
Gevraagd:
een oude boer wil aan elk van zijn drie kinderen een even groot stuk grond schenken. Daarvoor moet hij het volgende gebied in drie gelijke delen verdelen.
Het gebied heeft de vorm van de bovenkant van een parabool met vergelijking y = -(1/2) (x-4)2 +8 Het wordt aan 1 kant begrensd door een rivier. De boer wil het stuk grond zo eenvoudig mogelijk verdelen, maar wel zo dat elk van zijn kinderen een deel krijgt dat aan de rivier grenst. Hoe kan hij te werk gaan? (Op de tekening loopt de grafiek tot aan de x-as, de rivier begint juist onder de x-as)
Zelf weet ik niet hoe hieraan te beginnen? Ik dacht eraan om gewoon de bepaalde integraal te bereken en te delen door 3, maar hoe voer ik dan de voorwaarde in dat alle delen aan de rivier moeten grenzen?Ann
5-10-2005
Als ik het goed begrijp is de rivier het gedeelte onder de x-as:
Ik heb twee verticale lijnen aangegeven die als grens tussen de gebieden zouden kunnen gelden.
Er zou dan moeten gelden 0òtydx=1/3*0ò8ydx en uò8ydx=1/3*0ò8ydx.
hk
5-10-2005
#40627 - Integreren - 3de graad ASO