WisFaq!

Straal van de ingeschreven cirkel

Van een driehoek ABC is de oppervlakte gelijk aan 300 cm², de omtrek is 300 cm, bereken de straal van de ingeschreven cirkel?

petronella
16-8-2002

Antwoord

Als je vanuit het middelpunt van de ingeschreven cirkel verbindingslijnstukken trekt naar de 3 hoekpunten, dan splits je de hele driehoek op in 3 deeldriehoeken.



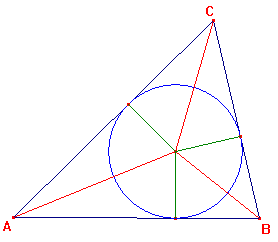
In elk van deze 3 driehoeken is de straal r van de ingeschreven cirkel meteen ook de hoogtelijn.

De oppervlakten van de 3 deeldriehoeken zijn dan resp.

$\frac{1}{2}·AB·r$ en $\frac{1}{2}·BC·r$ en $\frac{1}{2}·AC·r$

Bij elkaar opgeteld is dit $\frac{1}{2}·r·(AB + BC + AC)$ ofwel $\frac{1}{2}·r·omtrek$

Maar tevens is de optelsom van de oppervlakten van de 3 deeldriehoeken natuurlijk óók gelijk aan de oppervlakte $O$ van de volledige driehoek.

Conclusie: $\frac{1}{2}·r·omtrek = O$ ofwel $\eqalign{r=\frac{O}{halve\,\,omtrek}}$

MBL
16-8-2002