WisFaq!

Tophoek berekenen in kegel

Goedemiddag,
Ik zit met een probleem. Ik ben al een paar uur aan het zoeken voor het berekenen van de tophoek in een kegel voor willekeurige grondvlak en hoogte, maar ik vind geen formule daarvoor. Zouden jullie mij aub willen helpen?

sonny
7-9-2005

Antwoord

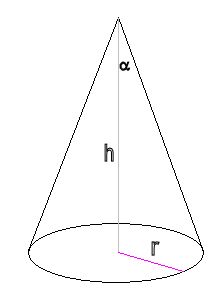
Stel de oppervlakte van het grondvlak is A.
A hangt samen met de straal van het grondvlak, volgens A=$\pi$r².
dus r=√(A/$\pi$)

de tophoek is gelijk aan 2 keer $\alpha$,
En voor hoek $\alpha$ geldt dat
tan$\alpha$ = r/h = {√(A/$\pi$)}/h

nu kun je dus de tophoek 2$\alpha$ uitrekenen.

groeten,

martijn

mg
7-9-2005