WisFaq!

Afhankelijkheid

Van een groep van 200 personen blijkt iedereen òf bloedgroep AB òf bloedgroep O te hebben.
Van elk van deze personen is de resusfactor bekend.
a)Toon aan dat de gebeurtenissen 'bloedgroep AB' en 'Rhesusfactor positief' afhankelijk zijn.
b)Welke getallen zouden er voor de nummer 15, 155, 5 en 25 moeten staan in het geval van volmaakte onafhankelijkheid.

Gegevens:
AB/Rh+: 15 Rh+ totaal: 170
AB/Rh-: 5 Rh- totaal: 30
O/Rh+: 155 AB totaal: 20
O/Rh-: 25 O totaal: 180

Jacqueline
15-8-2002

Antwoord

Maak eens een tabelletje (dat had trouwens ook bij je vraag over de TBC gekund).
Om de getallen enigszins onder elkaar te krijgen zet ik wat puntjes ertussen.

Er zijn 4 groepen te onderscheiden:

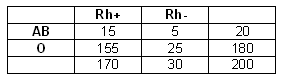
De gebeurtenissen AB en Rh+ zijn statistisch onafhankelijk als de volgende regel geldt:

P(AB én Rh+) = P(AB) x P(Rh+)

Volgens de tabel zou dan moeten gelden:

15/200 = 20/200 x 170/200.
Dit is niet waar, dus vervalt de onafhankelijkheid. Vandaar heet het afhankelijk. Probeer je bij het begrip "onafhankelijk" niet al teveel aan de letterlijke betekenis van het woord te binden of er bijv. medische verklaringen bij te halen. Het komt er gewoon op neer dat je de bovenvermelde vermenigvuldiging controleert.

De tweede vraag kan je bijv. op de volgende manier doen. Neem dezelfde tabel als daarnet, maar noem de aantallen nu x (voor AB en Rh+) en dus 20 - x (voor AB en RH-)
De andere aantallen zijn dan 170 - x en 10 + x.

Volledige onafhankelijkheid heb je nu als de twee kolommen (of de 2 rijen) in dezelfde verhouding liggen. Dat zou dan betekenen dat x/(20 - x) = (170 - x)/(10 + x).

Als je dit kruislings vermenigvuldigt valt (gelukkig!) de x² weg en vind je x = 17. Daarmee zijn alle aantallen bekend.

Eenvoudiger loopt het als volgt:

aan de getallen 20 en 180 zie je dat de tweede rij 9 keer zo groot is als de bovenste rij.
Het getal 170 moet je daarom verdelen in de verhouding 20 : 180 = 1 : 9 en dús komt er op de bovenste rij eerst 1/10 x 170 = 17 enz.
Deze aanpak is erg doorzichtig en lukt bij kleine tabellen meestal erg goed.
Aan jou de keuze wat je het simpelst vindt.

PS. leuk vak hé, die kansrekening!

MBL
15-8-2002