WisFaq!

Op hoeveel manieren kan je n personen in p groepen indelen?

Hallo,

Op hoeveel manieren kan je n personen in precies p groepen indelen? Bij voorbeeld: bij 4 personen in 3 groepen kan het op 6 manieren: AABC ABAC ABCA ABBC ABCB en ABCC.

Marcel K
23-7-2005

Antwoord

Eens kijken of ik dit begrijp. Je hebt 4 personen en je verdeelt ze in 3 groepen. Laten we de personen 1 t/m 4 noemen en de groepen A, B en C. Jouw oplossing is dan:

1. AABC
GROEP A: 1,2
GROEP B: 3
GROEP C: 4

2. ABAC
GROEP A: 1,3
GROEP B: 2
GROEP C: 4

3. ABCA
GROEP A: 1
GROEP B: 2,3
GROEP C: 4

4. ABBC
GROEP A: 1
GROEP B: 2,4
GROEP C: 3

5. ABCB
GROEP A: 1
GROEP B: 2
GROEP C: 2,4

6. ABCC
GROEP A: 1
GROEP B: 2
GROEP C: 3,4

Kennelijk is volgorde van de groepen niet van belang en moet er in elke groep minstens één persoon zitten.

Dit lijkt (bijna) op Op hoeveel manieren kun je 16 unieke knikkers verdelen over 8 knikkerpotjes?

Toepassen van dat antwoord levert:



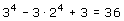
Maar omdat de 'volgorde' van de groepen niet uitmaakt, zou je nog even moeten delen door 3! (het aantal volordes van 3 groepen). Dus 36/3!=6

Nog maar eens voorbeeld:

Neem aan: ik heb 6 personen en 4 groepjes... Op geheel analoge wijze zou je dan dit moeten krijgen:



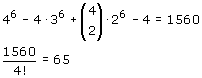
..en dat zou je dan zelf even moeten controleren...

Meer in 't algemeen zou je als algemene formule kunnen afleiden:



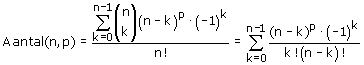
Wat ik dan toch wel weer bijzonder vind, als ik tenminste verder geen rare dingen heb gedaan... kijk maar 's of 't klopt! Ik ben er zelf nog niet zeker van...

WvR
27-7-2005