WisFaq!

Een boom aan de andere oever van een rivier

Het vraagstuk gaat als volgt:

Een persoon ziet van op de oever van een rivier de top van een boom op de andere oever onder een hoek van 60°. De persoon verplaatst zich 20 m achteruit ( in hetzelfde horizontaal vlak) en ziet de boomtop nu onder een hoek van 30°. Het oog van de waarnemer bevindt zich 1,60m boven de grond. Hoe hoog is de boom en hoe breed is de rivier?

Ik had gevonden dat de rivier 20 m breed was, maar dit lijkt niet te kloppen. Dus doe ik nu beroep op jullie.

Alvast dank bij voorbaat,

Steven

Steven De Keukeleire
18-7-2005

Antwoord

Ik neem aan dat die hoeken van 60° en 30° met een horizontaal vlak zijn.
Noem h de hoogte van de top van de boom boven dit horizontale vlak.
Noem de breedte van de rivier r.
Zie onderstaande tekening.

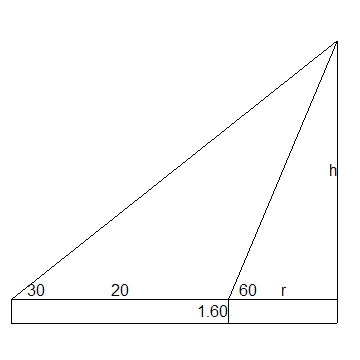
We krijgen dan h/r=tan(60°)=Ö3, dus h=rÖ3.
h/(r+20)=tan(30°)=1/Ö3, dus h×Ö3=r+20.
Conclusie: Ö3×Ö3×r=r+20
3r=r+20
r=10 en h=10Ö3
De breedte van de rivier is dus 10 meter en de hoogte van de boom is 1.60+10Ö3 meter.
Valt wel mee toch?

hk
18-7-2005