WisFaq!

Re: Bepaal de cartesische vergelijking

Bedankt voor de uitleg! Vraag 1 heb ik mooi verder kunnen uitwerken, maar bij vraag 2 ben ik onzeker over het verder verloop... de uitdrukkingen voor x, y en z apart schrijven, bedoel je daarmee ze als eerste rij zetten in een matrix mer eronder de coordinaten gelijk aan 0 gesteld?
Is het mogelijk me dat even voor te doen. Ik zou heel dankbaar zijn! Groetjes, Elia

Elia
13-6-2005

Antwoord

Beste Elia,

De vectoriële vergelijking van de rechte die we gevonden hadden, (-1,2,3) + k(2,3,-1), is equivalent met de volgende parametervoorstelling:



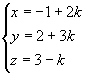
Hieruit kan je eventueel de parameter k elimineren maar eigenlijk kan het ook eenvoudiger. De carthesische vergelijking van een rechte wordt immers ook gegeven door:

(x-x₀)/a = (y-y₀)/b = (z-z₀)/c

Hierbij is (x₀,y₀,z₀) een punt van de rechte en (a,b,c) een richtingsvector, of stel richtingsgetallen.

Gewoon invullen levert nu:

(x+1)/2 = (y-2)/3 = (z-3)/(-1)

Als je de vergelijking wil in de vorm van een stelsel, als snijlijn van 2 vlakken, dan werk je de bovenstaande gelijkheiden uit via een kruisproduct.

mvg,
Tom

td
13-6-2005