WisFaq!

Voorwaardelijke kans

A en B zijn gebeurtenissen met
P(A)= 1/3, P(B)= 1/4, P( AÈB)= 1/2
Bereken: P(A|Ø B)

Ik heb gevonden dat dat gelijk is aan
(P(AÇØ B))/P(Ø B)

P(Ø B)= 1-P(B)
1-1/4= 3/4

(P(AÇØ B))/P(Ø B)= P(A)·P(Ø B)
= 1/3 · 3/4= 1/4

® (1/4)/(3/4)= 1/3

Is dit juist of moet ik dit op een andere manier oplossen?

Kim
26-5-2005

Antwoord

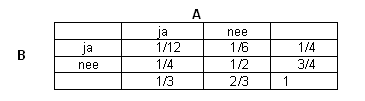
't Is niet zo gek... ik vind een tabelletje als hieronder in dit soort gevallen altijd wel handig...



Maar volgens mij heb je aardig door hoe 't werkt en lekker stoeien met de formules is natuurlijk ook altijd erg leuk...

WvR
27-5-2005