Bedoeld worden dan getallen die geschreven worden als quotiënt van een geheel getal a en een natuurlijk getal b. Dus a wordt gekozen uit de verzameling { ...-3, -2, -1, 0, 1, 2, 3....} en b uit de verzameling {1, 2, 3, 4, 5....}
Door de teller als geheel getal te mogen kiezen, worden negatieve rationale getallen mogelijk.
Simpele voorbeelden zijn dan: ¾, -2/23, 11/7, 0/4, 5/1 enz.
Het kenmerk van deze getallen is dat, wanneer ze decimaal geschreven worden, de decimalen op een bepaald moment stoppen óf vanaf een bepaald punt gaan repeteren.
Als je 'stoppen' uitlegt als 'het cijfer 0 gaat repeteren' dan kun je dus alles samenvatten onder de rubriek: de decimalen gaan op een bepaald moment repeteren.
Voorbeelden: 1/4 = 0,25 of eventueel 0,2500000....
4/9 = 0,4444444.....
3/37 = 0,081081081081.....
Overigens hoeft het repeteren niet meteen na de komma te beginnen!
Voorbeeld: 269611/8325 = 32,3857057057057....
Irrationale getallen zijn de getallen waar de decimalen nooit stoppen en ook nooit gaan repeteren.
Voorbeelden: p, e, sin12°, log25,
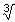 (-16)
(-16) Het aantonen dat een getal niet-rationaal is, is niet altijd eenvoudig en er zijn bepaalde regelmatig voorkomende getallen waarvan men het (nog) niet met 100 % zekerheid weet. Bedenk dat een computer misschien moeiteloos honderduizenden decimalen kan ophoesten zonder dat er een repeterend patroon te zien is, maar dat dat niets bewijst! Het repeteren kan namelijk misschien daarna nog beginnen.
MBL
13-7-2002