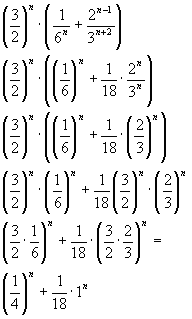WisFaq!

Limiet

Hoi,

Ik kreeg de volgende vraag voorgeschoteld:

lim[n->] ((3/2)^n) · (1/(6^n) + 2^(n-1)/3^(n+2))

nu dacht ik aan het volgende

(3/2)^ =
1/(6^) = 0 en
(2^(-1)/3^(+2)) = 1/18 · (2^/3^)

dus · (0 + 1/18 · (2^/3^))
Hierna kom ik er niet meer uit. Ik vind het altijd een beetje vreemd om over na te denken!

Grz,
Bart

PS: Is er niet een of andere tag dat ik een plaatje mee kan linken? Dit zou namelijk een stuk duidelijkere functies geven!
PPS: Ik heb misschien wel ergens een functie liggen waarmee je de tag op de plek van de cursor zet als je op het knop je klikt, maar dat moet ik nog even nakijken!

Bart van der Vliet
11-7-2002

Antwoord

Het klopt dat het lastig is om met ¥ te werken.
Bij dit soort opgaven moet je dit dan ook zo lang mogelijk uitstellen. Blijf met n werken, totdat je zeker weet wat er gebeurt als n naar ¥ gaat.
In jouw geval werkt dat als volgt:



Wanneer je nu de limiet van n naar ¥ neemt, gaat de eerste term naar 0 en de tweede term naar ¹/₁₈.
De totale limiet is dus ¹/₁₈.

wh
11-7-2002