WisFaq!

Diophantische vergelijking

Hoe los ik op:
0,5 x + 3 y + 10 z = 100 en x + y + z = 100 waarbij x,y,z gehele en positieve getallen zijn

Thomas
10-7-2002

Antwoord

Normaal zou je deze (nog) niet op kunnen lossen. In het geval van 3 (algemeen: n) onbekenden heb je ook 3 (algemeen: n) vergelijkingen nodig om het eenduidig op te kunnen lossen.

Maar omdat over het gehele positieve getallen gaat kan je dit probleem ook zonder derde vergelijking oplossen.



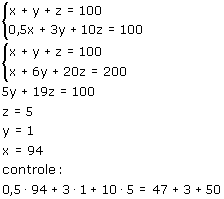
De 'grap' zit in 5y+19z=100. Omdat y en z gehele getallen zijn moet z wel 5 zijn, anders kom je nooit op honderd uit. Dus z=5, dan is y=1 en moet x=94 (samen honderd).

Zie Dieren en euro's vergelijking [http://www.wisfaq.nl/showrecord3.asp?id=1755]

WvR
11-7-2002