WisFaq!

Continuiteit functie volgens epsilon/delta-definitie

Hallo,
Stel functie (x^2-4)/(x-2). Het domein van deze dom f = R\{2}.
Op zicht (en volgens boek) is deze functie niet continu in zijn domein.
De definitie zegt echter "een functie is continu als de functie continu is voor alle x van adh dom f.
Nu is voor x = 2, een element van adh dom f, de functie is daarin onbepaald (maar zijn limiet bestaat wel..) dan is de functie toch wel continu volgens de epsilon-delta definitie? want f]x-delta,x+delta[ is deelverz. van ]f(x)-epsilon,f(x)+epsilon[ ?

Kan iemand opheldering geven, aub? Is de functie wel of niet continu?

Hadji Elea
17-5-2005

Antwoord

Hallo,

De definitie die je hanteert is in deze verwoording misschien wat onvolledig.
Opdat een functie f continu zou zijn in een punt a moeten er 3 (die zich eigenlijk herleiden tot 2) voorwaarden voldaan zijn:
- lim(x-a) f(x) moet bestaan
- F moet gedefinieerd zijn in a = a zit in dom f
- lim(x-a) f(x) = f(a)

Aan die eerste voorwaarde is wel voldaan, maar niet aan de anderen.

Met andere woorden: een functie f is continu in a indien de limietwaarde gelijk is aan de functiewaarde.
Gebruik maken van de epsilon-delta-definitie ziet dat er zo uit:



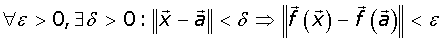
mvg,
Tom

td
17-5-2005