WisFaq!

Vergelijking parabool

Een parabool heeft de rechte met vgl x-3y-1=0 als as. Ze raakt aan de Y-as in het punt (0,1). Stel de vergelijkinge van de parabool op...

Sam
8-5-2005

Antwoord

Beste Sam,

Erg eenvoudig lijkt die oefening ons op het eerste zich niet en ook over de aanpak zijn we het niet helemaal eens geraakt, misschien zijn er wel meerdere manieren.

Helaas ken ik niet direct een formule om een verband te leggen tussen de symmetrie-as en een willekeurige parabool, dus wordt het was knutselwerk...
Ik toon alvast een eerste poging, als het nog anders (makkelijker) lukt hoor je het wel.

Ik vertrek van de algemene vergelijking van een kegelsnede:
ax² + by² + cz² + 2dyz + 2exz + 2fxy = 0

Voor een parabool moet hier gelden dan f² = ab maar ik veronderstel eerst a ¹ 0 zodat we hierdoor kunnen delen en alvast één onbekende kwijtspelen, ik houdt verder dezelfde letters maar dit zijn uiteraard niet de coëfficiënten van daarnet.
x² + by² + cz² + 2dyz + 2exz + 2fxy = 0

Voor een parabool moet nu gelden dat: f² = b en ik substitueer b, weer een onbekende kwijt:
x² + f²y² + cz² + 2dyz + 2exz + 2fxy = 0

De vergelijking van een raaklijn in een punt P wordt gegeven door de formule: (K is de functie van de kegelsnede)
x*¶K/¶x (P) + y*¶K/¶y (P) + z*¶K/¶z (P) = 0

Hierbij bedoel ik met (P) dat de partiële afgeleide geëvalueerd moeten worden in P. We vullen deze formule in voor ons raakpunt (0,1) (reken de afgeleiden zelf maar na) en stellen z intussen gelijk aan 1, we vinden voor de vergelijking van de raaklijn aan K in (0,1):
x(e + f) + y(d + f²) + c + d = 0

We weten dat deze vergelijking gelijk moet zijn aan de y-as, dus aan x = 0
Hieruit volgt dat de coëfficiënt van y en de constanten 0 moeten zijn, en dus het volgende stelsel:

| d+f² = 0 = d = -f²
| d+c = 0 = c = -d = f²
(Noot: x mag niet wegvallen dus moet ook e¹-f)

We substitueren c en d door de gevonden waarden in f en houden nog 2 onbekende coëfficiënten over:
x² + f²y² - 2f²y + 2ex + 2fxy + f² = 0

We weten dat (0,1) op de parabool ligt. Dit invullen heeft echter geen zin meer vermits we al van de raaklijn gebruik hebben gemaakt, alles zal gewoon wegvallen dus daar kunnen we niets uithalen. We weten echter wel dat het spiegelpunt van (0,1) t.o.v. de rechte óók op de parabool ligt, maar daarvoor moeten we dus eerst het punt spiegelen.

Je kunt daarvoor de overgang-matrices opstellen, dat gaat als volgt: neem een richtingsvector van de rechte (3,1) een een vector die er loodrecht op staat (1,-3). Deze vectoren vormen de kolommen van matrix M. Bepaal dan ook M^-1. De transformatie matrix voor een lijnspiegeling heeft is een diagonaalmatrix met elementen 1 en -1, ik noem deze even T. De coëfficiëntenmatrix wordt dan gegeven door M*T*M^-1 en dit is:
A =

De rechte heeft echter ook een constante, die matrix B kan je bepalen door een fixpunt te nemen (punt dat op de spiegelas ligt, bvb (1,0)), daarvoor moet immers gelden dat:
AX+B = X als je als X dit fixpunt neemt. Dit kan je oplossen naar B en je vind als matrix voor de constanten:


Transformatieformules:

*

+

Toegepast op het punt (1,0) vinden we dat ook (4/5,-7/5) op de parabool moet liggen. Als we dat invullen in onze laatste vergelijking van K en oplossen naar e vinden we:
e = -(18f² - 7f + 2)/5

Dit kunnen we invullen en we hebben nog maar één onbekende:
x² + f²y² - 2f²y - 2(18f² - 7f + 2)/5)x + 2fxy + f² = 0 of:
5x² + 10fxy - 2x(18f²-7f+2) + 5f²y² - 10f²y + 5f² = 0

Om de laatste onbekende f weg te krijgen snijdt ik de parabool nu met de spiegelas x = 3y + 1:
5(3y+1)² + 10f(3y+1)y - 2(3y+1)(18f²-7f+2) + 5f²y² - 10f²y + 5f² = 0 of:
5y²(f²+6f+9) - 2y(59f²-26f-9) - 31f²+14f+1 = 0

Dit is een vierkantsvergelijking in y die je in functie van f kan oplossen met de abc-formule. Van een parabool weten we dat ze altijd 2 snijpunten heeft, ofwel samenvallend (raakpunt) (discriminant = 0), ofwel toegevoegd imaginair (D0) ofwel verschillend reëel (D0).
We weten dat we zeker één reëel snijpunt hebben (de top) maar dit is geen raakpunt. Het andere punt moet, logischerwijs, op oneindig liggen. De noemers van de 2 oplossingen stel je gelijk aan 0 (anders kan je nooit oneindig bekomen). Dit is:
5(f² + 6f + 9) = 0 = f = -3

Uiteraard mogen niet beide oplossing oneindig geven, onze enige hoop is dat f = -3 ook een nulpunt van één van de 2 tellers is (dan krijg je 0/0 en in de limiet evt een reëel snijpunt). Blijkbaar hebben we nog geen fouten gemaakt (hoop ik toch) want we vinden inderdaad één keer a/0 (met a¹0) dus y = ¥ en de andere oplossing geeft 0/0, maar in de limiet voor f - -3 vinden we y = -4/15, dit zal de top van de parabool zijn.

De enige mogelijkheid is dus dat f gelijk is aan -3, ingevuld geeft dit voor onze kegelsnede:
x² - 6xy - 74x + 9y² - 18y + 9 = 0

Grafiek:


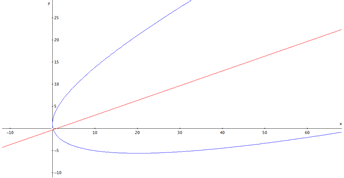
Het is een aardig uitwerking geworden en ik vermoed dat er een makkelijkere (kortere) manier moet zijn, maar ik kom er niet zo direct op...

mvg,
Tom

td
12-5-2005