WisFaq!

Driehoeken in een regelmatige negenhoek

Vanuit een punt P binnen een regelmatige negenhoek worden lijnen getrokken naar de hoekpunten. De negen driehoeken worden genummerd 1,2,..,9. Het totaal opp. van nr. 1 en 4 en 7 is gelijk aan het totaal opp. van 2 en 5 en 8, en aan dat van 3 en 6 en 9.
Dat betekent dus dat de som van de hoogtelijnen uit de genoemde driehoeken gelijk is. Verschuif je het punt dan verandert de totaalwaarde niet. Hoe dit te bewijzen ? rotatie ?

Henk Boxma
27-4-2005

Antwoord

In onderstaande figuur is ABCDEFGHK de bedoelde regelmatige 9-hoek, met zijde a.

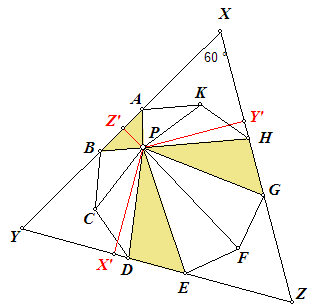
Het niet moeilijk aan te tonen, dat de lijnen AB, DE, GH een gelijkzijdige driehoek XYZ vormen.
De hoogtelijnen van de driehoeken PAB, PDE, PGH (PZ', PX', PY') zijn de afstanden van het punt P tot de zijden van XYZ.
Nu is de oppervlakte van XYZ (en van de op dezelfde manier verkregen andere twee gelijkzijdige driehoeken, bij 2,5,8 en bij 3,6,9) constant; zeg, in de drie gevallen, gelijk aan k.
De oppervlakte van XYZ is, voor zekere r, ook gelijk aan
¹/₂PZ' · ra + ¹/₂PX' · ra + ¹/₂PY' · ra = ¹/₂ra · (PZ' + PX'+ PY')
Zodat ook PZ' + PX'+ PY' constant is (gelijk aan 2k / ra).
En dit geldt dus voor elk punt P bij de driehoek XYZ (en bij die twee andere).
Dus geldt het ook voor elk punt P bij de bedoelde 9-hoek.

dk
27-4-2005