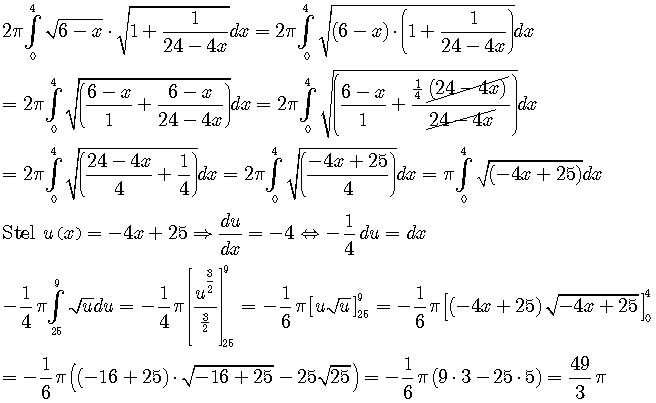
Davy
23-4-2005
Ik moet de zijdelingse oppervlakte die beschreven is door de grafiek van f berekenen:
f(x)= Ö(6-x) over (0,4) en bij wenteling om x
S= ò2pÖ(6-x)Ö(1+(f'(x))2) dx
f'(x)= -1/(2Ö(6-x))
(f'(x))2= 1/(24-4x)
Nu moet ik dit invullen in de integraal maar hoe los ik deze integraal dan op?
Kim
22-4-2005
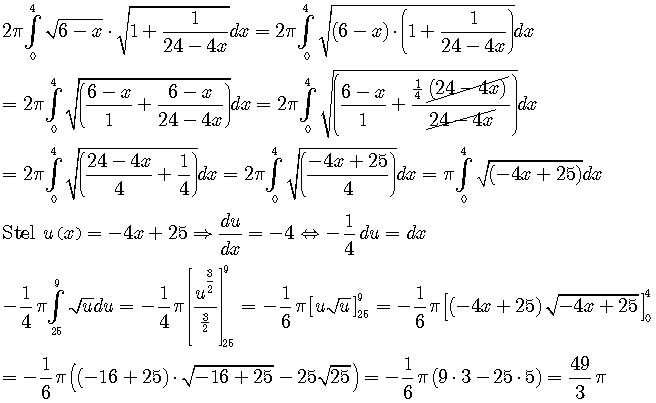
Davy
23-4-2005
#37143 - Integreren - 3de graad ASO