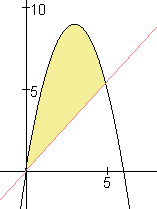WisFaq!

Oppervlakte berekenen

Ik heb problemen met de volgende opgaven, ik heb de oefeningen nog eens hermaakt maar ik weet niet waar het schoentje wringt?

(1)
Bepaal een rechte L door de oorpsrong die het gebied tussen y=-x²+6x en x-as in twee gebieden verdeelt met dezelfde oppervlakte.

f(x)=-x²+ 6x en y=kx
totale oppervlakte = 36 (via integralen berekent tussen x=0 en x=6 )

-x²+6x-kx=0
$\Leftrightarrow$ x=0 v x=6-k
We hebben eerst de oppervlakte onder de rechte van 0 tot (6-k) Dit is een driehoek dus:
([6-k)(6-k)]/2 (=0pp I)

Dan is er nog een stukje over van (6-k) tot 6, dit is een stukje van de parabool, oppervlakte II

oppII= (6 -$>$ 6-k)$\int{}$(-x²+6x)dx

Dus: oppI + oppII= gehalveerde opp
$\Leftrightarrow$ ([6-k)(6-k)]/2 + 6 -$>$ 6-k)$\int{}$(-x²+6x)dx = 18
$\Leftrightarrow$ 18+ ¹/₂k² -6k - (6³/3 - (6-k)³/3) + 6(6²/2 - (6-k)²/2 ) = 18
$\Leftrightarrow$ -k³+ $\frac{7}{2}$k²- 6k + 144=0
$\Leftrightarrow$ k=6,238.... ? (ik heb via mijn grafische rekenmachine het nulpunt van de bovenstaande vergelijking trachten te bepalen)

Wat deed ik fout? De juiste oplossing zou zijn:
rico L=-3³√4 +6

(2)
Bepaal een rechte L evenwijdig met de X-as, die het egbied tussen y= -x²+9 en de X-as in twee gebieden verdeelt met dezelfde oppervlakte.

Ik deed het volgende:

f(x)= -x² +9 en y=k
totale oppervlakte = 36 (via integralen berekent tussen x=-3 en x=3 )

-x² +9 = k
$\Leftrightarrow$ x= +/- √ (9-k)

De grafiek van de functie is volledig symmetrisch dus het volstaat de ene helft te berkenen en vermenigvuldigen met 2.

We bereken eerst de oppervlakte onder de rechte tussen x=0 en x=√ (9-k)

Dit is een rechthoek dus oppervlakte I = k.√ (9-k)

Het tweede gedeelte van de oppervlakte gaat van
x=√ (9-k) tot x=-3 onder de parabool dus.

Dit berekenen we a.d.h.v.e integraal:

(√ (9-k) -$>$-3)$\int{}$ (-x²+9)dx

Dus, de halve oppervlakte =

2·oppI + 2·oppII = 18
$\Leftrightarrow$ 2k√+ 2·(- (-√(9-k)³)/3 + (-3)³/3 - 9√(9-k) + 27 ) = 18

$\Leftrightarrow$ (2k + 6 -²/₃k - 18)√(9-k) +18=0
$\Leftrightarrow$ (4k - 12)√(9-k)=-18
$\Leftrightarrow$ √(9-k) = -18/($\frac{4}{3}$k-12)
$\Leftrightarrow$ -16/9 k³ - 16k² - 432k + 972 = 0
$\Leftrightarrow$ k= 2,057.... ? (ik heb opnieuw via mijn grafische rekenmachine het nulpunt van de bovenstaande vergelijking trachten te bepalen)

De juiste oplossing zou moeten zijn: y= 9- (9/2)³√2 ?

Kan iemand me hiermee verder helpen aub?

Alvast bedankt...

Veerle
2-4-2005

Antwoord

Het is handiger de 'bovenste helft' te nemen. De oppervlakte van het gele stuk is inderdaad 18. Je kunt dan met de rechter grens x=6-k de oppervlakte van het gele stuk uitrekenen... en daar komt 18 uit. Je krijgt zoiets als: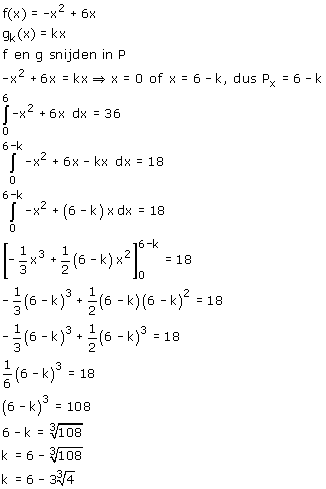



Bij voorbeeld 2 kan je kijken naar de integraal van -x²+9 met de grenzen -Ö(9-x) en Ö(9-x). Je krijgt dan:



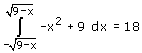
Probeer 't maar eens...

WvR
2-4-2005