WisFaq!

Vierdegraads formule berekenen

We hebben een grafiek van een vermoedelijk vierdegraads functie. Hoe moeten we de formule hierbij berekenen?
de verschilfunctie van de hellingsfunctie is ongeveer 0,5x-2. Hoe moeten we hierbij de formule van de helling berekenen en hoe moeten we daarna verder?

Leerling X
8-6-2002

Antwoord

Dit kan met het interpolatiepolynoom van Lagrange: zijn van een funtie f, n+1 steunpunten gegegeven, dan kunnen we door deze n+1 steunpunten een ondubbelzinnig bepaald polynoom p(x) van de graadn aanbrengen.

Voorbeeld
Gegeven 5 punten A(0,1), B(1,3), C(2,-3), D(3,4) en E(4,-2).
Dat polynoom zal er dan zo uit zien:



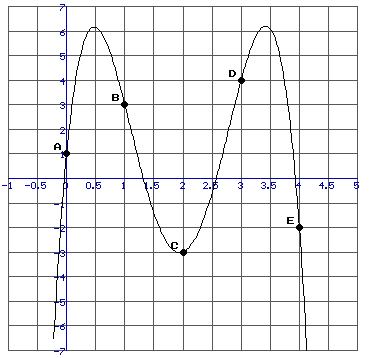
Daarmee heb je uiteraard nog niet het functievoorschrift van deze (vierdegraads?) functie te pakken.

Laten we zeggen f(x)=ax⁴+bx³+cx²+dx+e, hiermee kunnen we schrijven:
f(0)=1 Þ e=1
f(1)=3 Þ a+b+c+d+e=3
f(2)=-3 Þ 16a+8b+4c+2d+e=-3
f(3)=4 Þ 81a+27b+9c+3d+e=4
f(4)=-2 Þ 256a+64b+16c+4d+e=-2
Hieruit zou je (in principe) de waarden van a,b,c,d en e moeten kunnen uitrekenen.

Maar gelukkig zit er op je GR (TI83) iets als QuarticReg. Zet de punten in L1 en L2:

L1  L2
0   1
1   3
2  -3
3   4
4  -2

Toets vervolgens:
STAT
CALC
QUARTREG L1,L2
en je GR geeft keurig:
a=-1,9583...
b=15,25
c=-36,0416...
d=24,75
e=1
en daarmee heb je een benadering voor het functievoorschrift van deze vierdegraadsfunctie te pakken. Handig toch?

WvR
9-6-2002