WisFaq!

Regeloppervlak

Hoe kan ik bewijzen dat x²+y²-z²=1 een regeloppervlak is? x=1 & y=z dit is een rechte lijn door de punten (1,1,1) & (1,2,2) & (1,3,3)

x²/a²+y²/b²-z²/c²=1 hoe kan ik daarvan een aantal punten geven?

x y z
2 0 0
0 3 0

Amanda
8-6-2002

Antwoord

Om te bewijzen of x²+y²-z²=1 een regeloppervlak is, zou je een parametrisering moeten kunnen vinden van de vorm:

x(u,v)=b(u)+v·d(u) (1)

b(u) en d(u) zijn krommen in de ruimte. Op onderstaande website kun je voorbeelden vinden. En volgens mij staat jouw 'oppervlak' er ook bij: the elliptic hyperboloid!
Zie http://mathworld.wolfram.com/EllipticHyperboloid.html

In jouw geval wordt dat:



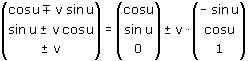
Deze parametrisering voldoet in ieder geval aan (1), maar ook aan x²+y²-z=1

Hopelijk kan je hier verder mee.

Zie Rules Surface [http://mathworld.wolfram.com/RuledSurface.html]

WvR
15-6-2002