De top van de tetraŽder ligt precies recht boven het zwaartepunt M. M ligt op BN (een zwaartelijn), zodat BM=2∑NM.
Zie ook De oppervlakte en inhoud van een tetraŽder
WvR
11-2-2005
Wat bedoelt u precies met het volgende?! :
"Nu moet je alleen nog even gebruiken dat de top van de piramide recht bůven het zwaartepunt van het grondvlak ligt en dat dat zwaartepunt de zwaartelijn verdeelt in de verhouding 1:2"
Dat snap ik niet helemaal...Charlotte
10-2-2005
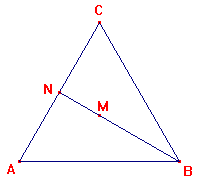
Kijken we naar 'het grondvlak' van een tetraŽder (een gelijkzijdige driehoek!):
De top van de tetraŽder ligt precies recht boven het zwaartepunt M. M ligt op BN (een zwaartelijn), zodat BM=2∑NM.
Zie ook De oppervlakte en inhoud van een tetraŽder
WvR
11-2-2005
#33903 - Ruimtemeetkunde - Leerling bovenbouw havo-vwo