WisFaq!

Bewijs van de overstaande zijden

Ik heb een vraag bij het bewijs van de overstaande zijden.

De opdracht is: Als de diagonalen van vierhoek ABCD loodrecht op elkaar staan, dan is de som van de kwadraten van twee overstaande zijden gelijk aan de som van de kwadraten van de andere twee overstaande zijden. Bewijs.

Ik hoop dat je deze vraag kan bewijzen.
Jasper

Jasper Goyvaerts
1-2-2005

Antwoord

Beste Jasper,

Ik heb even een schets gemaakt van een volledig willekeurige vierhoek waarvan de diagonalen loodrecht zijn.
Elke zijde heeft een letter, en de letters bij de diagonalen hebben enkel betrekking tot het gedeelte van de diagonaal waar ze bij staan (dus niet de volledige diagonalen, tot aan het snijpunt).



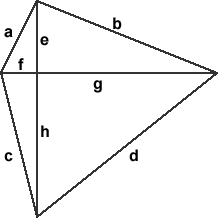
Nu zie je duidelijk dat er 4 rechthoekige driehoeken gevormd zijn waarin Pythagoras geldt:
a² = e² + f²
b² = e² + g²
c² = f² + h²
d² = g² + h²

Bekijk nu de sommen van de kwadraten van de overstaande zijden a²+d² en b²+c²:
a²+d² = e² + f² + g² + h²
b²+c² = e² + g² + f² + h²

Deze zijn gelijk

mvg,
Tom

td
1-2-2005